Aller au contenu

Nombres complexes

Définition#

Théorème#

  • On admet l'existance d'un ensemble de nombres appelé nombres complexes : \(\mathbb{C}\), contenant \(\mathbb{R}\) l'ensemble de tous les réels.
  • \(\mathbb{C}\) est muni de deux opérations élémentaires, l'addition et la multiplication.
  • \(\mathbb{C}\) comporte un nombre noté \(i\), le nombre imaginaire, tel que \(i^2 = -1\).
  • Tout élement \(z\) de \(\mathbb{C}\) possède une écriture unique sous la forme \(z = a + ib,\:(a ,b) \in \mathbb{R}^2\)
Exemples de nombres complexes
  • \(3x\)
  • \(\sqrt{15}\)
  • \(2i\)
  • \(x + 2i\)
  • \(\frac{\sqrt{x + 2}}{3} - 3i\)

Remarque

Dans \(\mathbb{C}\) on définit des opérations comme dans \(\mathbb{R}\), mais pas de relation d'ordre comme \(x > y\). Il est alors faux de noter \(z \geq z'\) si \(z\) et \(z'\) sont deux nombres complexes non réels.

Vocabulaire#

  • Dans la notation d'un nombre complexe, on trouve deux parties distinctes, la partie réelle et la partie imaginaire. Prennons \(z = a + ib\), ici \(a\) est la partie réelle et \(b\) la partie imaginaire.
  • La forme algébrique du nombre complexe \(z\) s'écrit sous la forme \(z = a + ib\)
  • Si la partie réelle d'un nombre complexe est nulle, donc \(a = 0\), on dit qu'il s'agit d'un nombre imaginaire pur.
Propriété

On dit que deux nombres complexes \(z\) et \(z'\) sont égaux si et seulement si leurs parties réelles et imaginaires sont égales :

\[ \begin{cases} z = a + ib\\ z' = x + iy \end{cases} \]
\[ z = z' \Leftrightarrow \begin{cases} a = x\\ b = y \end{cases} \]

On note aussi qu'un nombre complexe est nul si et seulement si sa partie réelle et sa partie imaginaire sont nulles.

Représentation géométrique#

Oui il faut un peu parler de géométrie pour mieux se représenter un nombre complexe. Prennons le plan \(P\), muni d'un repère orthonormé \((O; \vec{i}; \vec{j})\), ainsi que le point \(M(2; 3)\) :

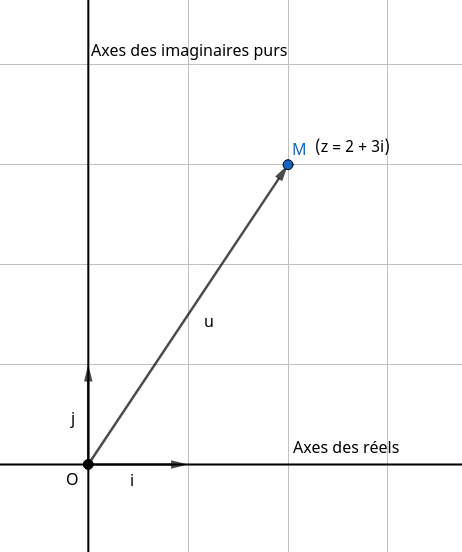
Plan complexe

Propriété

À tout nombre complexe \(x = a + ib\), on associe :

  • un point \(X(a; b)\) sur le plan \(P\).
  • un vecteur \(\vec{v}(a; b)\).

On dit que \(M\) est l'image de \(z\), et inversement, \(z\) est l'affixe de \(M\). On dit aussi que \(z\) est l'affixe du vecteur \(\vec{u}\).

Calculs d'affixes#

  1. Soient \(A\) et \(B\) deux points d'affixes \(z_{A}\) et \(z_{B}\).

    L'affixe du vecteur \(\vec{AB}\) vaut \(z_{\vec{AB}} = z_{B} - z_{A}\).

    L'affixe du milieu \(M\) du segment \([AB]\) vaut \(z_{M} = \frac{z_{A} + z_{B}}{2}\).

  2. Soient deux vecteurs du plan \(P\), \(\vec{u}(z)\), \(\vec{v}(z')\) et un nombre réel \(k\).

    L'affixe du vecteur \(\vec{w} = \vec{u} + \vec{v}\) vaut \(z + z'\).

    L'affixe du vecteur \(k\vec{u}\) vaut \(kz\).

Forme trigonométrique#

Définitions#

Définition

Soient \(z = a +ib\) un complexe non nul dans le repère orthonormé \((O; \vec{i}; \vec{j})\) et son image \(M\).

  • On appelle module de \(z\) le nombre réel positif noté \(|z| = \sqrt{a^2 + b^2}\). Il s'agit aussi de la norme du vecteur \(\vec{OM}\).
  • On appelle argument de \(z\) la mesure en radians de l'angle \((\vec{i}; \vec{OM})\), noté \(arg(z)\).
Propriétés des modules

\(\forall (z, z') \in \mathbb{C}^2\) :

  • \(|z|^2 = z \times \overline{z}\)
  • \(|zz'| = |z| \times |z'|\)
  • \(|\frac{z}{z'}| = \frac{|z|}{|z'|}, \forall z' \ne 0\)
Propriétés des arguments

\(\forall (z, z') \in \mathbb{C}^2, (z, z')\) non nuls et \(\forall n \in \mathbb{Z}\) :

  • \(arg(\overline{z}) = -arg(z)\)
  • \(arg(zz') = arg(z) + arg(z')\)
  • \(arg(z^n) = n \times arg(z)\)
  • \(arg(\frac{z}{z'}) = arg(z) - arg(z')\)
Remarque
  • \(arg(-z) = arg(z) + arg(-1) = arg(z) + \pi\)
  • \(arg(\frac{1}{z}) = arg(1) - arg(z) = - arg(z)\)

Forme trigonométrique#

La forme trigonométrique du nombre complexe \(z\) est \(z = |z|(\cos(arg(z)) + i\sin(arg(z)))\). En posant \(r = |z|\) et \(\theta = arg(z)\), on obtient :

\[ z = r(\cos\theta + i\sin\theta) \]

On utilisera l'identité trigonométrique pythagoricienne pour passer un nombre complexe de sa forme algébrique à sa forme trigonométrique, et inversement.

Exemple

Donner la forme trigonométrique du nombre complexe \(z = 1 + i\).

La forme trigonométrique de \(z\) est de la forme \(z = r(\cos\theta + i\sin\theta)\).

Calcul du module de \(z\) :

\[ r = |z| = \sqrt{a^2 + b^2} = \sqrt{1^2 + 1^2} = \sqrt{2} \]

Calcul de \(\cos\theta\)1 :

\[ \cos\theta = \frac{a}{r} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]

Calcul de \(\sin\theta\)2 :

\[ \sin\theta = \frac{b}{r} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]

Déduction de \(\theta\)3 :

\[ \theta = \frac{\pi}{4} \]

Au final, la forme trigonométrique du nombre complexe \(z\) est :

\[ z = \sqrt{2}(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}) \]

Remarque : en simplifiant cette forme on retrouve bien la forme algébrique initiale \(z = 1 + i\).

Forme exponentielle#

La forme exponentielle d'un nombre complexe \(z\), avec \(r = |z|\) et \(\theta = arg(z)\) est \(z = re^{i\theta}\)

En effet les propriétés des arguments d'un nombre complexe justifient la notation exponentielle.

Propriétés

\(\forall (\theta, \theta') \in \mathbb{R}^2\), \(\forall n \in \mathbb{N}\) :

  • \(e^{i\theta} \times e^{i\theta'} = e^{\theta + \theta'}\)
  • \((e^{i\theta})^n = e^{in\theta}\)
  • \(\frac{e^{i\theta}}{e^{i\theta'}} = e^{i(\theta - \theta')}\)

Le conjugué#

Exemple

Pour \(z = 3 + 4i\), \(\overline{z} = 3 - 4i\) Pour \(z = \sqrt{3} - \frac{3}{4}i\), \(\overline{z} = \sqrt{3} + \frac{3}{4}i\)

On note \(\overline{z} = a - ib\) le conjugué de \(z = a + ib\).

Propriétés

\(\forall (z, z') \in\mathbb{C}^2, n \in \mathbb{N}\):

  • \(\overline{z + z'} = \overline{z} + \overline{z'}\)
  • \(\overline{zz'} = \overline{z} . \overline{z'}\)
  • \(\overline{\frac{z}{z'}} = \frac{\overline{z}}{\overline{z'}}, z' \ne 0\)
  • \(\overline{z^n} = \overline{z}^n\)

Le conjugué d'un nombre complexe est son symétrique par rapport à l'axe des abscisses (axe des réels).

Équation du second degré#

Pour les équations du second degré nous étions bloqués en cas de discriminant négatif. En effet la fonction racine carrée étant définie sur \([0 ; +\infty[\), un discriminant réel négatif rend alors l'expression \(\frac{- b \pm \sqrt{\Delta}}{2a}\) impossible à résoudre dans \(\mathbb{R}\).

Cependant, dans \(\mathbb{C}\) il est tout à fait envisagable de résoudre une ESD avec un discriminant négatif.

Nous avons alors comme solutions de l'équation \(az^2 + bz +c = 0\), avec toujours \(\Delta = b^2 - 4ac\) :

  • Si \(\Delta > 0\) :

\(z_{1} = \frac{-b + \sqrt{\Delta}}{2a}\) et \(z_{2} = \frac{-b - \sqrt{\Delta}}{2a}\)

  • Si \(\Delta = 0\) :

\(z_{0} = \frac{-b}{2a}\)

  • Si \(\Delta < 0\) :

\(z_{1} = \frac{-b + i\sqrt{-\Delta}}{2a}\) et \(z_{2} = \frac{-b - i\sqrt{-\Delta}}{2a}\)

Exemple

Résolvons l'équation \(f(z) = 0\) dans \(\mathbb{C}\), avec :

\[ f(z) = 2z^2 - 3z + 6 \]

Il s'agit d'une ESD, nous allons déterminer la ou les solutions possibles dans \(\mathbb{C}\) de \(f(z) = 0\).

Calcul du discriminant :

\[ \Delta = b^2 - 4ac = (-3)^2 - 4(2 \times 6) = -39 \]

Nous trouvons un discriminant négatif. L'équation \(f(z) = 0\) comprend deux solutions conjuguées dans \(\mathbb{C}\) : \(z_{1} = \frac{-b + i\sqrt{-\Delta}}{2a}\) et \(z_{2} = \frac{-b - i\sqrt{-\Delta}}{2a}\).

Calcul de la première racine :

\[ z_{1} = \frac{-(-3) - i\sqrt{-(-39)}}{2 \times 2} = \frac{3 - i\sqrt{39}}{4} \]

En découle alors la seconde :

\[ z_{2} = \frac{3 + i\sqrt{39}}{4} \]

Au final, l'équation \(f(z) = 0\) admet deux solutions dans \(\mathbb{C}\) :

\[ S = \{\frac{3 - i\sqrt{39}}{4} ; \frac{3 + i\sqrt{39}}{4}\} \]

Exercices#

Un jour peut-être. Avec des corrigés en plus.

Sources

  1. Utilisation de l'identité trigonométrique pythagoricienne \(\cos\theta = \frac{adjascent}{hypothénuse}\). ↩

  2. Utilisation de l'identité trigonométrique pythagoricienne \(\sin\theta = \frac{opposé}{hypothénuse}\). ↩

  3. Voir les valeurs remarquables trigonométriques. ↩